TOTP algorithm: by example
Note: A version of this post was previously published as part of coursework for the subject SCIE90012 (Science Communication).
At some stage, you may have entered a 6-digit code from a 2FA app like Google Authenticator. But where did this code come from?
The answer lies within the QR code and the inner workings of the Time-based One-time Password algorithm (TOTP).
Here is an example of the algorithm in action.
The preparations
To prepare, I performed a MFA reset on my university account.
This was the QR code:
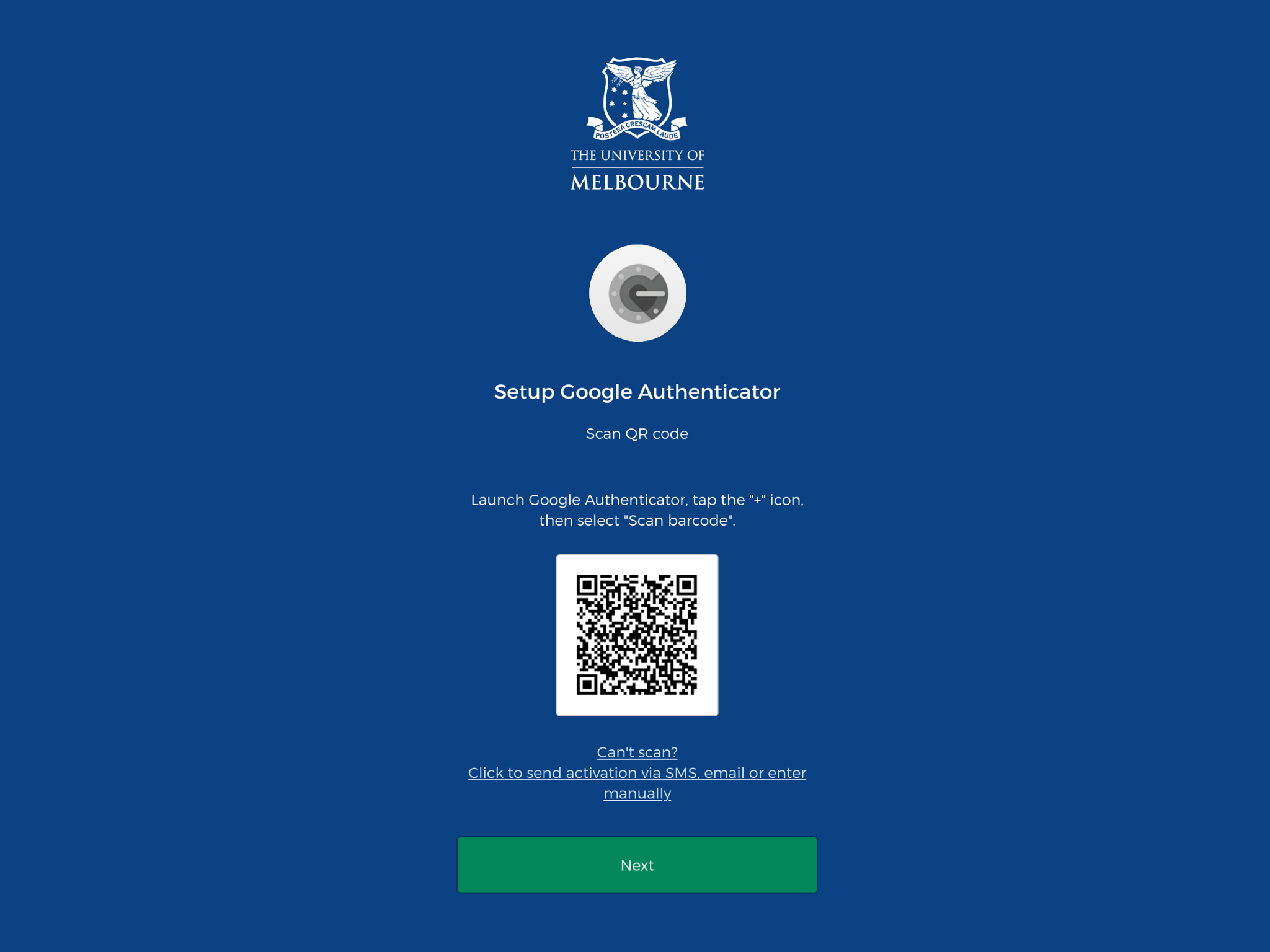
Then, I enrolled the QR code into my 2FA app and took the following screenshot on the 27th of September, at 9:21:19 pm UTC+10 Australia/Melbourne time:
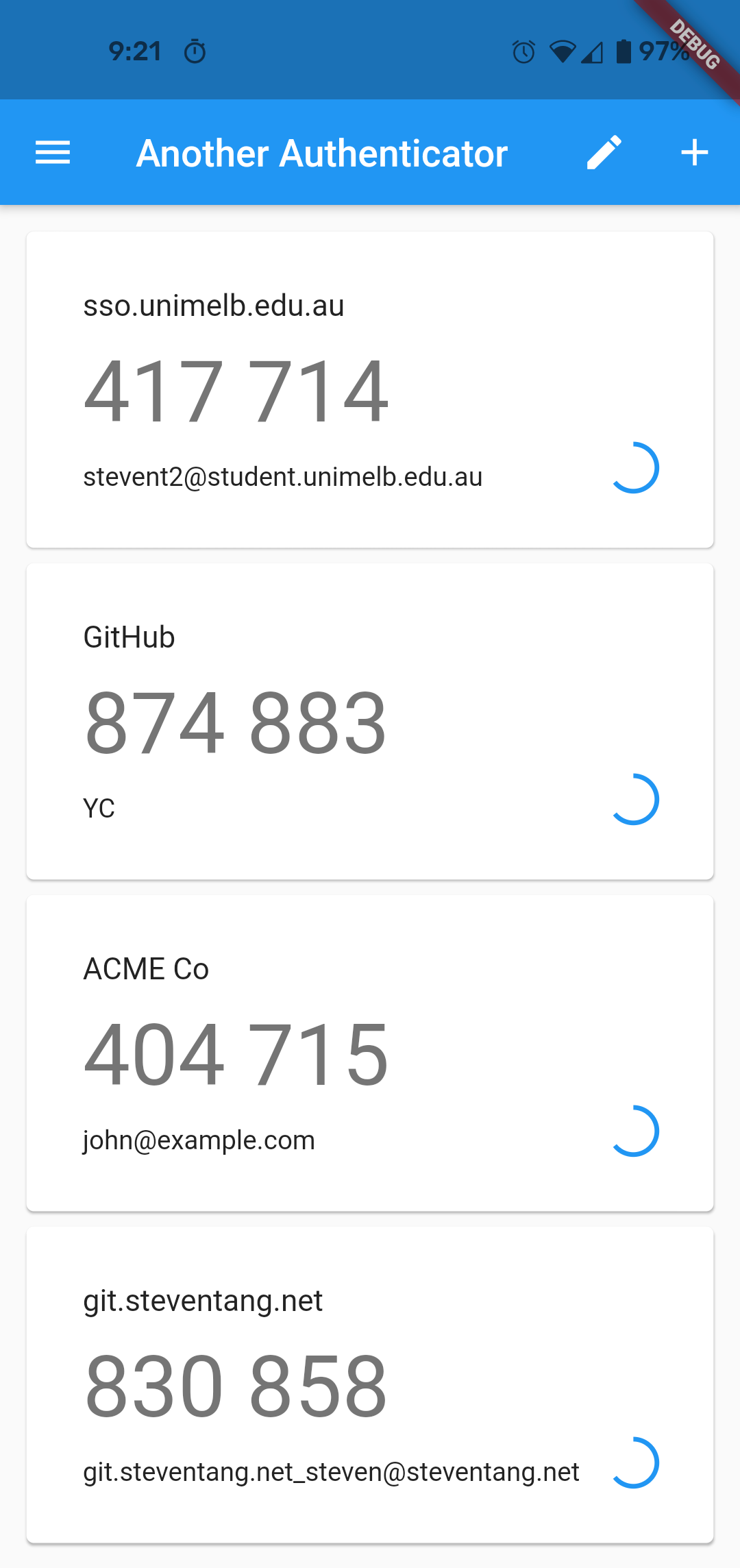
With this, we have all the information necessary to recompute and verify the code.
Decode the QR
First, we must decode and make sense of the QR.
I’ve used a decoder to find the following URI:
otpauth://totp/sso.unimelb.edu.au:stevent2%40student.unimelb.edu.au?secret=XE7ZREYZTLXYK444&issuer=sso.unimelb.edu.au
From the URI, we see that the secret is XE7ZREYZTLXYK444.
The time?
Time undoubtedly plays an important role in the TOTP algorithm, which is defined as TOTP = HOTP(K, T), where K is the secret key and T = (Current Unix Time - T0) / X, with floor division being applied.
Current Unix Time is an integer counting the number of seconds (excluding leap seconds) since the unix epoch (January 1st, 1970). The date above converts to 1632741679 (18897 days, (21 - 10) hours, 21 minutes, 19 seconds).
T0 is the unix time from which counting starts and X is the time step in seconds, which controls how often the code changes. By default, T0 is the unix epoch (the value 0) and X is 30 seconds (if not specified).
This, along with the use of floor division means that T will stay the same across every 30 second period for this example.
Substituting in these values, we get the counter value T = (1632741679 - 0) / 30 = 54424722.
HOTP
From before, we have K = XE7ZREYZTLXYK444 and T = 54424722. By default, HOTP uses HMAC-SHA1. Taking K and T, HMAC-SHA1(K, T) produces an irreversible fixed-size value (a hash) from the input.
Convert the secret
The secret is in Base32, which uses the digits A-Z and 2-7 to represent the values 0-25 to 26-31 respectively.
- Convert from Base32 digits to decimal (e.g. using a lookup table).
X E 7 Z R E Y Z T L X Y K 4 4 4 23 04 31 25 17 04 24 25 19 11 23 24 10 28 28 28 - Convert decimal to binary (each will be less or equal to 5 bits, because values 0-31 are represented).
10111 00100 11111 11001 10001 00100 11000 11001 10011 01011 10111 11000 01010 11100 11100 11100 - Rewrite this into groups of 4 bits, and convert binary to hexadecimal using the trick that 4 binary digits is one hexadecimal digit.
1011 1001 0011 1111 1001 1000 1001 0011 0001 1001 B 9 3 F 9 8 9 3 1 9 1001 1010 1110 1111 1000 0101 0111 0011 1001 1100 9 A E F 8 5 7 3 9 C
Convert the counter value
- Convert to binary and then hexadecimal.
54424722 = 0011 0011 1110 0111 0100 1001 0010 3 3 e 7 4 9 2 - Pad this number to 8 bytes (16 hexadecimal digits) by adding leading zeros, per the RFC.
00000000033e7492
HMAC & Truncation
With the converted values, we can calculate the SHA1-HMAC.
The values from above produces the following hash: 38056c8282a236a5ad624ff292b984d20138aba8.
Next, we follow a dynamic truncation algorithm to extract a section of the hash:
Given the 20 byte SHA1 hash String, extract the “low-order 4 bits of
String[19]” to use as Offset.
When splitting the hash into 20 segments,String[19]is the last segment (since we start from index 0). This isa8.
Then, because one hexadecimal digit represent 4 binary bits, and the least significant digit is the rightmost digit, it is8in this example.Convert the 4 bits into a number.
8 in hexadecimal is the same in decimal (base 10), and so we move on.Return the last 31 bits of
String[Offset]...String[Offset+3].
Substituting in 8, this becomesString[8]...String[11].38 05 6c 82 82 a2 36 a5 ad 62 4f f2 92 b9 84 d2 01 38 ab a8 0 1 2 3 4 5 6 7 ^ ^ ^ ^ 12 13 14 15 16 17 18 19We can then convert this into binary, by replacing each hexadecimal digit with its 4-digit binary equivalent.
a d 6 2 4 f f 2 1010 1101 0110 0010 0100 1111 1111 0010Since it’s the last 31 bits, we unset the first bit.
0010 1101 0110 0010 0100 1111 1111 0010
The next step involves converting this 31-bit binary number into decimal.
229 + 227 + 226 + 224 + 222 + 221 + 217 + 214 + 211 + 210 + 29 + 28 + 27 + 26 + 25 + 24 + 21 = 761417714
When not specified in the URI, 6-digit codes are used by default. Hence, we can (in the final step) write down the last six digits of the number.
And voila, 417714!
References
Verified with:
$ oathtool --totp --verbose --now "2021-09-27 11:21:19 UTC" --base32 XE7ZREYZTLXYK444
Hex secret: b93f9893199aef85739c
Base32 secret: XE7ZREYZTLXYK444
Digits: 6
Window size: 0
TOTP mode: SHA1
Step size (seconds): 30
Start time: 1970-01-01 00:00:00 UTC (0)
Current time: 2021-09-27 11:21:19 UTC (1632741679)
Counter: 0x33E7492 (54424722)
417714